这是一个流水帐吧, 随意记录.
在此之前(2019-09-02)也面过几家, 不过时间有点久, 就先不写了,如果日后偶尔想起来, 能补还是会回来补的.
算法部分
阿里笔试( 2019-08-30 )
阿里的笔试我没有参加, 这是我的一个同学参加了阿里的笔试, 他面完后在群里说了一个笔试题,我看了一下, 给出一个自己的解法.
题目如下
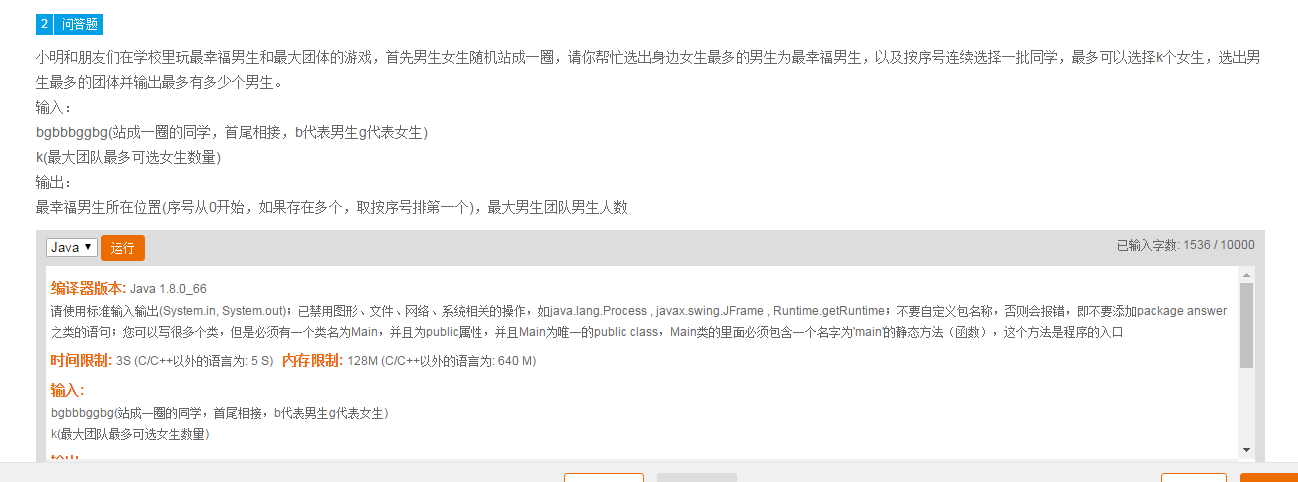
这个问题其实是两个不相干的问题, 最开始一看让人觉得是两个约束条件,但是其实不是, 这是两个问题....
我重述一下问题.
现在有一群男生女生, 随机围成一个圈, 然后从某个位置按序编号.
- 问题一: 找出身边女生最多的男生的编号, 换句话说, 就是问哪个男生周围女生最多.
- 问题二: 若连续选择多个人, 这多个人中最多包含 k 个女生, 那么选的这些人中最多有多少个男生.
这里问题的复杂性在于大家排队组成的是一个环, 但其实环这种问题可以通过取余来辅助解决.
思路是这样的, 我们遍历一遍输入, 然后分别用 girlidx 和 boyidx 存放女生男女生的索引,假设某个男生的索引为 boyidx[i], 那么前的男生索引则为 boyidx[i - 1],其后的男生索引则为 boyidx[i + 1]. 如下所示
boyidx[i-1] boyidx[i] boyidx[i+1]
只要我们算出 boyidx[i+1] 与 boyidx[i-1] 之间的距离, 那么计算 boyidx[i] 周围的女生个数就轻而易举,可以得到 boyidx[i] 周围的女生数目为
(boyidx[i+1] - boyidx[i-1] + 1) - 3
------------------------------- -
| |
| v
v remove the three boys
the number of boy between boyidx[i-1] and boy[i+1]
理想很丰满, 现实很骨感, 就像刚刚上面说的, 环引入了一些复杂性.当我们遍历到 boyidx[i] 时, i-1 可能越界, 除此之外, boyidx[i+1] - boyidx[i-1]并不难保证 boyidx[i+1] 就一定大于 boyidx[i-1], 所以可能引入负数, 这当然是不正确的,怎么解决呢, 取余数法.
举个例子, 我们按顺时针走下面这列输入
0 1 2 3 4 5 6 7
input b g b b g g b g
那么我们可以得到男生女生的索引坐标如下
girlidx 1 4 5 7
boyidx 0 2 3 6
我们想计算 boyidx[0] 的周围女生有多少, 于是
boyidx[0 + 1] - boyidx[0 - 1] - 2
|
v
boyidx[1] - boyidx[-1] - 2
负索引, C++ 里面这样算起来肯定凉凉. 实际上这里 boyidx[-1] 对应的应该就是boyidx[3], 即最后一个男生. 通过取余数我们可以这样来算
boyidx[(0 + 1 + boyidx.size()) % boyidx.size()] => boyidx[1]
boyidx[(0 - 1 + boyidx.size()) % boyidx.size()] => boyidx[3]
|
v
boyidx[1] - boyidx[3] - 2
|
v
2 - 6 - 2 ?
|
v
WTF?
看起来又遇到了负数问题, 不过这个好解决, 取余大法.
因为我们的 boyidx 得到的索引值都是位于所有人当中的, 所以我们应该加上整体人数,然后再对整体人数取余数. 我们记
total = girlidx.size() + boyidx.size()
如下
(boyidx[1] - boyidx[3] + total) % total - 2
|
v
(-4 + 8) % 8 - 2
|
v
2
于是我们正确的得到了 boyidx[0] 周围的女生个数. 至此第一问完美收工.
再来看第二问. 第二问其实和第一问本质上是一样的. 最多包含 k 个女生,那我们当然是包含越多女生越好, 如果 k 大于等于所有女生的个数,那么就返回所有人的数目减去女生的数目, 即可得到最多团体中男生的人数.
如果 k 小于最多女生的个数, 对于女生 i, 那么我们就计算 giridx[i-1] 和 giridx[i+k] 这两个女生之间的人数(不包含这两个女生), 那么得到的这个数值再减去 k 就得到了最多团体中男生的人数.
下面的代码在凌晨四点半写的, 可能有点 bug, 因为上面的思路是在睡觉时想到的,爬起来就写了一下, 时间复杂度 O(n), 看看就行.
#include <iostream>
#include <string>
#include <vector>
using namespace std;
inline int adjcounter(vector<int> &partial, int start, int end, int total) {
start = (start + partial.size()) % partial.size();
end = (end + partial.size()) % partial.size();
return (partial[end] - partial[start] + total) % total + 1;
}
int main() {
string input; int k; cin >> input >> k;
vector<char> people(input.begin(), input.end());
vector<int> girlidx, boyidx; for(int i = 0; i < people.size(); ++i) {
if(people[i] == 'g') girlidx.push_back(i);
else boyidx.push_back(i);
}
int happyman = -1, girls = 0;
for(int i = 0; i < boyidx.size(); ++i) {
int leftgirls = adjcounter(boyidx, i - 1, i, people.size()) - 2;
int rightgirls = adjcounter(boyidx, i, i + 1, people.size()) - 2;
// cout << "[+] " << i << " => " << leftgirls << " " << rightgirls << endl;
int curgirls = leftgirls + rightgirls;
if(happyman == -1) {
happyman = boyidx[i];
girls = curgirls;
}
if(curgirls > girls) {
happyman = boyidx[i];
girls = curgirls;
}
}
cout << happyman;
cout << " ";
if(k >= girlidx.size()) {
cout << people.size() - girlidx.size() << endl;
return 0;
}
// Now, k is less than girlidx.size()
int maxcount = 0;
for(int i = 0; i < girlidx.size() - k; ++i) {
int leftmen = adjcounter(girlidx, i - 1, i, people.size()) - 2;
int rightmen = adjcounter(girlidx, i + k, i + k + 1, people.size()) - 2;
int mencount = leftmen + rightmen + adjcounter(girlidx, i, i + k - 1, people.size());
if(mencount > maxcount) {
maxcount = mencount;
}
}
cout << maxcount - k << endl;
return 0;
}
/*
0 1 2 3 4 5 6 7
b g b b g g b g
*/