题目意思:给一个字符串s,求其最大回文子串.你可以认为字符串s的最大长度是1000.
回文呢,应该很好理解,我记得小学时候语文上的"上海自来水来自海上",从左到右以及从右到左读都是一样的.特别的情形是, 如果一个字符串为空或者只有一个字符,那么我们也认为是回文.
暴力枚举实在是走投无路时的下下之策,但"又不是不能用"(严肃认真脸).枚举的时间复杂度是$O(n^3)$. 那么这个时间复杂度怎么计算出来的呢?尽管可以完全跳过去这个计算,但,用数学语言无懈可击的描述出来,这难道不是一件很cool的事情么?
对于长度为n的字符串,枚举的思想就是$\forall i,j(i \geq j)\in [0,n-1]$,检测所有的[i,j]区间是否为回文. 它的时间复杂度可以按下面的式子进行计算(忽略了检测s[i,j]是否为回文串的历程),也就是$$\sum_{i=0}^{n-1} \sum_{j=0}^{i} (i-j+1) $$
这个式子初看起来似乎有些可怕,但毛主席说过,这都是纸老虎!在此我强烈推荐Donald等人所写的Concrete Mathematics一书, 里面专门有一节讲的就是对求和$\sum$式子的一些展开和变换,相当精彩.当然上面这个式子用不着多么高深的知识.求内部和时, 将i视作常数,那这样的话,就是一个等差数列啦.于是上面的式子就变成了$$ \sum_{i=0}^{n-1} 1+2+3+\cdots+(i+1)= \sum_{i=0}^{n-1}\frac{(i+1)(i+2)}{2}=\sum_{i=0}^{n-1}\frac{i^2+3i+2}{2}$$
而这里的主要部分就是$i^2$求和了,有: $$\because \sum_{i=1}^{n} i^2 = \frac{n(n+1)(n+2)}{6} \hspace{2cm} \therefore \sum_{i=0}^{n-1} i^2 = \frac{(n-1)n(n+1)}{6}$$ 于是,时间复杂度为$O(n^3)$.1)i>=j ==> ★单个字符串或空字符串,则dp[i][j]=true; 2)i<j ==> ★当且仅当s[i..j]为回文串且s[i-1]==s[j+1]时,dp[i-1][j+1]=true ★其他情况dp[i-1][j+1]=false
核心部分就是中间那条,由s[i..j]推理s[i-1...j+1].然后就是写代码啦,如下:
#include <iostream> #include <cstring> #include <algorithm> using namespace std; class Solution { public: string longestPalindrome(string s) { int n = s.length(); //动态申请空间 char **dp = new char*[n]; for(int i = 0;i < n; ++i) { dp[i] = new char[n]; memset(dp[i],'1',sizeof(char) * n); } //记录要返回的回文串的:开始索引,结束索引,长度 int beg = 0,end = 0,len = 1; //由于是计算dp[i+1][j-1],因此i要先算大的,j要先算小的 //因此i从大到小遍历,j从小到大遍历 for(int i = n - 1; i >= 0; --i) { for(int j = 0; j < n; ++j) { //回文串长度为1 if(i >= j) { dp[i][j] == '1'; continue; } //cout<<i<<"\t"<<j<<"\t"<<dp[i + 1][j - 1]<<endl; if(dp[i + 1][j - 1] == '1' && s[i] == s[j]) { dp[i][j] == '1'; if(len < j - i +1) { len = j - i + 1; beg = i,end = j; } continue; } dp[i][j] = '0'; } } //释放空间 for(int i = 0;i < n; ++i) delete [] dp[i]; delete[] dp; return s.substr(beg,end - beg + 1); } }; //=======================Driver=========================== int main() { Solution sol; string s("abcda"); cout<<sol.longestPalindrome(s)<<endl; return 0; } /* ===========complexity============== Time Complexity:O(n^2) Space Complexity:O(n^2) ===========makefile================= all: @g++ solve.cpp -o solve @./solve clean: rm -f solve reset ===========leetcode accepted======== 93 / 93 test cases passed. Status: Accepted Runtime: 162 ms Submitted: 0 minutes ago ===========submission date========= 2017.01.10 */
在上面的代码中,你可以看到是由前一个状态dp[i+1][j-1]状态求dp[i][j],实际上原理是一样的,纯属个人习惯问题.这样写的话, 需要确定循环如何写,因为是dp[i+1][j-1]求dp[i][j],所以dp[i+1][j-1]的状态相对于dp[i][j]应该是已知的,那么i就应该从大向小循环, j就应该从小向大循环.
由于是求最大的回文串,那么我们可以用一个变量len来记录当前已知的回文串长度,然后不断更新,并用beg和end分别记录当前已知最大回文串的起始和结束索引.
记录dp状态时,我用了字符数组而不是整形数组,这样的话适当的省一些空间,但是注意赋值以及判断时要写成对应字符形式的0和1.
动态规划法的时间复杂度应该是一眼就能看出来的,为$O(n^2)$,空间复杂度也是$O(n^2)$.
这样,上面的代码就应该很好理解且很容易写出来了.
除了上面的解法,还有一种比较优秀的解法是后缀树,时间复杂度可以达到O(nlogn).但Manacher这个炫酷的解法,可以用O(n)时间解决掉. 真是很拽很拽,给人的感觉就是这样的:

心里跟我默念"Anyone else?",一定要大声念.感受到那种雄赳赳气昂昂过跨过鸭绿江, 打美国大兵的霸气了么!不要在公共场合大声喧哗,毕竟你是学算法的,否则你可能会被打的 .(严肃脸).
这个算法不好理解,但国外有人写的很清楚了,你来这里 [PART-1 and PART-2] 看看,这是我在网上找到的最贴近就差"手把手"教你的讲解了.最终我是看懂了.我就在这里写下我的理解,如果有益于你理解该算法那最好不过了.
这里的第一个问题就是判断一个字符串是否为回文串,我们需要分奇数偶数的情况,该问题的解决方法很容易理解,但是不容易想到. 对任意长度为n的字符串,我们可以认为每个字符左右是有空隙的,那么当我们把这些空隙填充完后,我们就可以拿着这个全新的字符串来分析. 这个新字符串的长度一定是奇数.因为长度为n的字符串,一定有n+1个空隙,那么填充后,新的字符串长度为2n+1.
这里的第二个问题,就是如何从已有的信息中获取未知的信息.这和KMP字符串模式匹配异曲同工(但KMP理解比这个理解要困难的多). 现在假如说我们已经知道了索引为m处的回文字符串,其左右边界分别为ml,mr.我们用d来表示LPS数组(d[i]表示索引i处的最长回文串长度), d[i]对应地反映在新数组中,其含义是相对于i处的左右边界偏移,理解这里的概念,对你正确编码至关重要.盗用geeksforgeeks上的一张图片, 借此说明相关概念,如下:
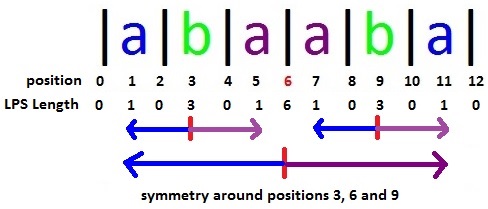
假如说m=6,我们已知m=6处的回文字符串信息,有LPS[6]=6,因此一方面可以认为原字符串中回文字符串的长度为6(再如position=0处,偏移为0,说明原回文串长度为0,因为原回文串不存在字符), 一方面可以也可以认为在新字符串中,左偏移6达到新字符串中回文串的左边界,右偏移6达到右边界.偏移是什么意思呢?对于任意的x,y,如果y-x=z,那么就说y相对于x的偏移为z. 这里说左偏移多少,就是减去多少,右偏移多少就是加上多少.
现在,将问题抽象出来,如下,我将把抽象出来的结合上面的实例来进行说明,你可以参照这两幅图进行理解:
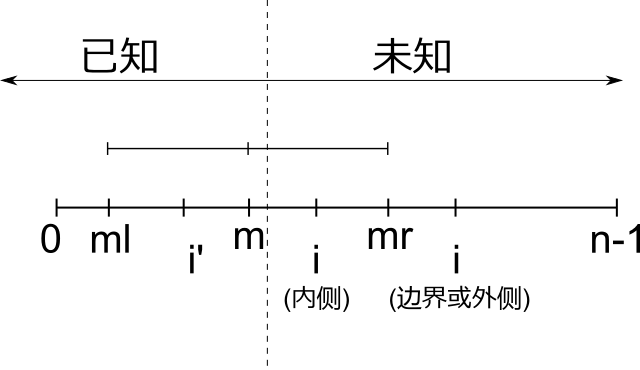
m处的回文字符串覆盖范围为[ml..mr],而[0,m]处的最大回文字符串我们都是已知的,现在要求的未知部分,仅有两种可能:
1)右边界之外的我们可以通过更新m(向右移动),在某个时候覆盖右边界之外所求处的字符时,再进行处理,暂时可以将其LPS设置为0, 因为LPS偏移至少为0.
2)右边界上的也应该先设置为0,为什么呢?尽管我们知道ml和mr一定是关于m对称的,而我们知道ml的情况,但是此时我们仅知道的是, 对于mr处的回文串,其左侧部分和ml处回文串右侧一定是对称相等的,但是mr处回文串右侧部分究竟是上面,则是无从得知的.因此, 根据已有信息,并不能更近一步确定其LPS>0,所以只能暂时设置为0.
3)如果说所求i位于内侧,我们记i'为i关于m的对称点(那么显而易见,有2m-i==i'),此时i'处的情况是完全已知的, 但此时也分两种情况,第一种是LPS[i']>=i'-ml=mr-i,这种情况下,我们仅能得知的是,i处的回文字符串覆盖范围至少不能低于i'处的回文串范围, 也就是说LPS[i]可以先设置为LPS[i'],然后进一步"精益求精".第二种是,LPS[i']<mr-i,那么此时可以肯定知道的是, i处的回文串一定覆盖在m处回文串的掩盖下.那么此时,LPS[i']=LPS[i].这两种情况都是取较小者, 因此可以方便的表示为LPS[i]=min(LPS[i'],mr-i)=min(LPS[2*m-i],mr-i)
现在最难的部分已经过去了,那么新的问题是,如何进一步精益求精?
最精妙的已经被我们想到了,那么只剩下一种方法了,那就是蛮力计算了.不过蛮力也是有瞎用力. 现在,我们已经能够确定回文串的一个"最小长度"了,那么我们应该从该最小长度向两侧同时枚举,按照回文串的定义进行求精.恩,就是这么简单.
还没有完,说好的mr边界外的呢?!我们还需要更新中心点m,那什么时候该更新呢?在计算出i处的最终值LPS值时,我们可以得到一个新的回文串覆盖范围, 如果发现大于m的右边界,那么此时就更新m.
空间复杂度为O(n),时间复杂度不好计算,但是我们可以这样来考虑,因为每次虽然我们是想两边拓展,但是每次检测的都是未知的领域, 可以认为是不断的向右侧单边未知领域的逐一扩展,时间复杂度为O(n).
#include <iostream> #include <cstring> #include <algorithm> using namespace std; class Solution { public: string longestPalindrome(string s) { int n = s.length(); if(n == 0) return s; //预处理,将字符串以'|'竖线分割开来 char split = '|'; string str(2 * n + 1,split); for(int i = 0;i < 2 * n + 1; ++i) if(i % 2 == 1) str[i] = s[(i - 1) / 2]; //LPS数组 int *d = new int[2 * n + 1]; memset(d,0,(2 * n + 1) * sizeof(int)); d[0] = 0; //初始中心点,右边界 int m = 0,mr = 0; //最大偏移,最大长度对应的元素索引 int dmax = 0,dindex = 0; for(int i = 1;i < 2 * n + 1; ++i) { //i'=2m-i //若d[i']<i'-ml=mr-i ==> d[i]=d[i'] //若d[i']>i'-ml=mr-i ==> d[i]>=mr-i,可取mr-i if(i < mr) d[i] = min(d[2 * m - i],mr - i); //当i>=mr时,取0 else d[i] = 0; //进一步调整d[i]为最终值,这里比较经典的一行代码 while(str[i - d[i] - 1] == str[i + d[i] + 1] ) { ++d[i]; //边界校验 if(i - d[i] - 1 < 0 || i + d[i] + 1 > 2 * n) break; } if(d[i] > dmax) { dmax = d[i];dindex = i; } //更新中心点m和右边界mr if(i + d[i] > mr) {m = i;mr = i + d[i];} } //返回值的边界值(dindex-dmax),(dindex+dmax) delete[] d; return s.substr((dindex - dmax) / 2,(dindex + dmax - (dindex - dmax) + 1) / 2); } }; //=======================Driver=========================== int main() { Solution sol; string s("cdbabcbabdbab"); /* |a|b|c|d <=索引转换=> abcd 0,1 0 2,3 1 4,5 2 所以(左/2)==>右 */ cout<<sol.longestPalindrome(s)<<endl; return 0; } /* ===========complexity============== Time Complexity:O(n) Space Complexity:O(n) ===========makefile================= all: @g++ solve.cpp -o solve @./solve clean: rm -f solve reset ===========leetcode accepted======== 93 / 93 test cases passed. Status: Accepted Runtime: 6 ms Submitted: 0 minutes ago ===========submission date========= 2017-01-12 Thu 11:40 PM */
如你所看到的,代码里面用的是以'|'来填充空隙,使用的是动态字符串数组,平均运行时间时6ms,由于leetcode说了,你可以假设最大长度为1000,如果你设置成静态LPS数组, 运行时间可能会更短.
上述代码中的这一句可能不是很好理解:
while(str[i - d[i] - 1] == str[i + d[i] + 1] ) if(i - d[i] - 1 < 0 || i + d[i] + 1 > 2 * n) break;为何要-1或者+1呢,因为我们计算的是判断i处字符两侧的情况,不用计算i处的字符(我们已经知道了一个最低下界就是d[i],如果不+1或-1, 那么会把最长回文串的长度多计算一次,导致错误发生).这里也注意要进行边界检测.
新旧字符串的索引是可以通过算数运算互换得到的,在测试函数main()中我有注释说明,你看一下就理解了,这里就不多说了.
如果到这里你还是不太明白,很正常,有一种万能之法,那就是多看几遍.....
罗伯特.塔扬(Robert Tarjan)教授是一位著名的计算机科学家,师从Donald Knuth,在CS领域取得了许多了不起的成就, 2012年4月12日到中国访问,在清华大学做了演讲,记者曾提问:您的一生取得了非凡的成就,在您看来,这些成就是天赋还是机遇? 他回答说,如果你研究的领域是和数学相关的,研究过程中失败是不可避免的,你可能会觉 得懊恼,甚至会用头撞墙,但是你一定要坚持下去.如果一个问题总是找不到答案,你可 以换一个课题去研究,然后过一段时间再来攻克这个难题.不管你有多么聪明,多么有天 赋,我认为毅力,以及不断的学习都是非常重要的.
科学家用脑袋"撞墙"才想出来的算法,我们难道不应该多理解几遍?
子串和子序列一样吗?废话,当然不一样.
子序列(subsequence)和子串(substring)的区别:void * memset ( void * ptr, int value, size_t num ); Sets the first num bytes of the block of memory pointed by ptr to the specified value (interpreted as an unsigned char). ptr Pointer to the block of memory to fill. value Value to be set. The value is passed as an int, but the function fills the block of memory using the unsigned char conversion of this value. num Number of bytes to be set to the value. size_t is an unsigned integral type.memset是将一个内存卡(ptr所指),该内存卡的每一字节均初始化为数值value,字节数为num.现在有一个需求,想把一个内存块全部值设置为1:
int *iptr = new int[n];memset(ptr,1,n*sizeof(int));//这个可以么? char *cptr = new char[n];memset(prt,'1',n*sizeof(char));//这个可以么?答案是,前者不可以,后者可以.为什么?Have a try and Find the truth.