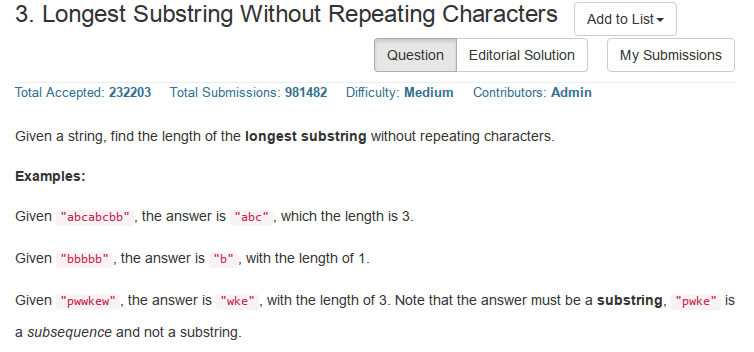
 题目意思:给一个字符串找到其最长的不重复子串.注意,子串和子序列是不一样的.
题目意思:给一个字符串找到其最长的不重复子串.注意,子串和子序列是不一样的.
#include <iostream> #include <string> using namespace std; class Solution { public: int lengthOfLongestSubstring(string s) { if(s.length() == 0) return 0; //字符串s的最长不重复子串长度 int maxlen = 1; //以j结尾的最长不重复子串长度 int jmaxlen = 1; for(int j = 1;j < s.length();++j) { int repeat = 0; for(int i = j - 1;i >= j - jmaxlen;--i) { //如果以j-1结尾的最长不重复子字符串含有s[j],且s[i]==s[j] //则以j结尾的最长不重复子字符串长度为j-(i+1)+1 if(s[i] == s[j]) { jmaxlen = j - (i + 1) +1; repeat = 1; break; } } //如果以j-1结尾的最长不重复子字符串不含有s[j],则s[i]==s[j] //则以j结尾的最长不重复子字符串长度为jmaxlen+1 if(!repeat) jmaxlen += 1; maxlen = maxlen > jmaxlen ? maxlen : jmaxlen; } return maxlen; } }; //=======================Driver=========================== int main() { Solution sol; string s("abcabcbb"); cout<<sol.lengthOfLongestSubstring(s)<<endl; return 0; } /* ===========complexity============== 记字符串长度为n Time Complexity:O(n^2)) Space Complexity:O(1) ===========makefile================= all: @g++ solve.cpp -o solve @./solve clean: rm -f solve reset ===========leetcode accepted======== 第一种: 983 / 983 test cases passed. Status: Accepted Runtime: 32 ms Submitted: 0 minutes ago 第二种 ===========submission date========= 2017-01-07 Sat 03:42 PM */
本题使用动态规划来解决,因此只要找到转移方程即可.
字符串s的最长的不重复子串一定位于字符串s中,不妨设该子串为s[i..j],如下图所示:
那么,如果我们记L[k]为以s[k]结尾的最长不重复字符串的长度,那么遍历整个字符串便可以得到数组L[0],L[1],...,L[n-1], 因此s的最长不重复字符串应是max{L[0],L[1],...,L[n-1]}.
接下来就是找L[k]与L[k+1]之间的关系.我们可以推出以s[k]结尾的最长字符串为ss=s[k-L[k]+1..k]:
状态方程搞定后代码就比较好写了.在写代码的时候,如果申请一个数组L专门来做存储,不是很值得, 我们可以只需要维护一个变量jmaxlen,用其存储j之前的最大子串长度(也就是以s[j-1]结尾的子串长度). 每遍历一个元素更新一次jmaxlen,再用另一个变量maxlen表示字符串s的当前已知的最大长度,用jmaxlen来更新. 那么当整个s遍历完之后,maxlen即为所求的值.
空间复杂度为O(1),而时间复杂度则考虑最坏情况,也就是s是本身就是其最大的不重复子串,那么总共需要比较 $$0+1+2+3+...+(n-1)=\frac{(n-1)n}{2}$$,因此时间复杂度为$O(n^2)$
#include <iostream> #include <string> using namespace std; class Solution { public: int lengthOfLongestSubstring(string s) { if(s.length() == 0) return 0; //字符串s的最长不重复子串长度 int maxlen = 1; //以j结尾的最长不重复子串长度 int jmaxlen = 1; for(int j = 1;j < s.length();++j) { int pos = find(s,j-jmaxlen,j-1,s[j]); if(pos == -1) jmaxlen += 1; else jmaxlen = j - (pos + 1) +1; maxlen = maxlen > jmaxlen ? maxlen : jmaxlen; } return maxlen; } int find(string s,int i,int j,char c) { //递归终止条件 if(i > j) return - 1; int mid = (i + j) / 2; //检测是否位于中间 if(s[mid] == c) return mid; //检测是否位于右侧 int right = find(s,mid + 1,j,c); if(right != -1) return right; //检测是否位于左侧 int left = find(s,i,mid - 1,c); if(left != -1) return left; //不在右侧,不在左侧也不在中间 return -1; } }; //=======================Driver=========================== int main() { Solution sol; string s("bbbbb"); cout<<s.length()<<endl; cout<<sol.lengthOfLongestSubstring(s)<<endl; return 0; }
然并卵,一提交,超时!!!后来一想,那个find函数算什么二分查找嘛?!,根本不是有序的!错因就在这里! 但是算法是正确的,就是时间啊,太多了,递归嵌套,增加了相当多的无用次数,导致时间极具增加.
这种奇葩思想,各位看官笑笑就好.